ARMA-Prozess

(Additive) Kombination eines AR (vgl. 19.34) und eines MA Prozesses (vgl. 19.41).

Auszug aus Wikipedia (http://de.wikipedia.org/wiki/ARMA-Modell)

$y_t=\epsilon_t + \sum_{i=1}^n a_i y_{t-i} + \sum_{j=1}^m b_j \epsilon_{t-j}$

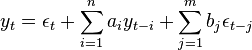
Dieses Modell wird auch als ARMA(n,m)-Modell bezeichnet, wobei n und m die Ordnung des Prozesses heißen.

Mit Hilfe des so genannten Verschiebungsoperators L (von lag=Zeitverschiebung):

$L^d x_t = x_{t-d}$

schreibt man kürzer auch:

$(1-\Phi(L))y_t = (1+\theta(L)) \epsilon_t$

wobei $\Phi$ und θ beides endliche Polynome (der Grade n und m) darstellen:

$\Phi(x) = \Phi_1 x+ \cdots + \Phi_n x^n$