Die Schiefe zeigt die Stärke der Asymmetrie einer Wahrscheinlichkeitsverteilung an. Bei einer symmetrischen Verteilung (wie Normalverteilung) liegt die Schiefe bei 0. Ist die Schiefe positiv (negativ), so ist die Verteilung rechtsschief (linksschief) und Werte, die kleiner (größer) sind als der Mittelwert, häufiger zu beobachten sind, als Werte über (unter) den Mittelwert (so dass sich der Gipfel (Modus/Modalwert, siehe 19.21) links (rechts) vom Mittelwert befindet), der rechte (linke) Teil des Graphs ist flacher als der linke.
Auszug aus Wikipedia (https://de.wikipedia.org/wiki/Schiefe_%28Statistik%29):
Die Schiefe (englischer Fachausdruck: Skewness bzw. Skew). Sie zeigt an, ob und wie stark die Verteilung nach rechts (positive Schiefe) oder nach links (negative Schiefe) geneigt ist. Jede nicht symmetrische Verteilung heißt schief.
Die Schiefe einer Zufallsvariable ist das zentrale Moment 3. Ordnung µ3(X) (falls das Moment 3. Ordnung existiert), normiert auf die Standardabweichung.
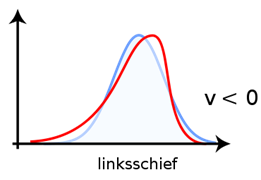
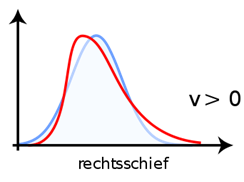
Abbildung 250: Beispiele für linksschiefe und rechtschiefe Verteilung (jeweils Rot) im Vergleich zu einer Normalverteilung (Blau)