Die Wölbung zeigt die Stärke der Spitze einer Wahrscheinlichkeitsverteilung im Vergleich zu einer Normalverteilung mit Standardabweichung 1 (wie die Standardnormalverteilung (siehe 19.18) an. Bei der Standardnormalverteilung (siehe 19.18) liegt die Wölbung bei 0. Ist die Wölbung positiv (negativ), so ist die Verteilung steilgipfig (flachgipfig) und Ausreißer (siehe 19.22) sind häufiger (seltener) als bei einer Standardnormalverteilung.
Auszug aus Wikipedia (https://de.wikipedia.org/wiki/W%C3%B6lbung_%28Statistik%29):
Die Wölbung, Kyrtosis, Kurtosis oder auch Kurtose (griechisch κύρτωσις kýrtōsis „Krümmen“, „Wölben“) ist eine Maßzahl für die Steilheit bzw. „Spitzigkeit“ einer (eingipfligen) Wahrscheinlichkeitsfunktion, statistischen Dichtefunktion oder Häufigkeitsverteilung. Die Wölbung ist das zentrale Moment 4. Ordnung. Verteilungen mit geringer Wölbung streuen relativ gleichmäßig; bei Verteilungen mit hoher Wölbung resultiert die Streuung mehr aus extremen, aber seltenen Ereignissen.
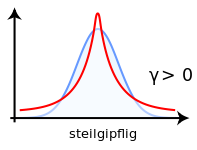
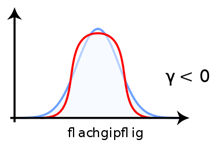
Abbildung 251: Beispiele für steilgipfige und flachgipfige Verteilungen (jeweils Rot) im Vergleich zu einer Normalverteilung (Blau)