Meistens ist es einfacher, grafisch aufbereitete Informationen zu interpretieren. Mit Hilfe eines Histogramms kann man sehr viele Informationen auf einem Blick darstellen, entsprechend können Histogramme bei der Interpretation von Ergebnissen sehr viel helfen. Nachfolgend werden einige Ideen aufgezeigt die bei der Interpretation von Histogrammen hilfreich sein können. Diese Liste erhebt keinen Anspruch auf Vollständigkeit.
• Breite
Sofort auf den ersten Blick wird sichtbar, wie breit das Histogramm ist. Dadurch bekommt der Betrachter ganz schnell ein Gefühl der Risikomenge.
Außerdem bekommt man sehr schön dargestellt, dass die einwertige Planung kaum Aussagekraft hat, denn die tatsächlichen Realisationen sehr vielfältig sein können.
• Asymmetrie / Schiefe / Überhang.
Meistens kann man aus der Form ganz schnell beurteilen, wie symmetrisch die Verteilung insgesamt ist, und dadurch bekommt man ein Gefühl für die Schiefe (ohne auf den sehr schwer interpretierbaren Wert der Schiefe zu blicken). Gleichzeitig sieht man aus der Asymmetrie auch die Höhe eines (evtl. vorhandenen) Gefahren- oder Chancenüberhang.
Die Beziehung zwischen Mittelwert und Planwert, die in der Grafik gleich sichtbar ist, gibt zusätzliche Information über die Asymmetrie. Liegt der Erwartungswert unter (über) dem Planwert, gibt es ein Gefahren- (Chancen-) Überhang (im Vergleich zur Planung). Fällt der Erwartungswert mit der Planung überein, sind Chancen und Gefahren symmetrisch um den Planwert verteilt, die Planung ist also erwartungstreu und entspricht den Anforderungen der GoP.
• Quantile / Extremwerte / Fat-Tails
In dem Histogramm ist gleich sichtbar, ob Extremwerte vorhanden sind, bzw. wie weit diese Extremwerte liegen bzw. wie wahrscheinlich diese sind. Weiterhin wird schnell klar, wo die Quantile insgesamt liegen, bzw. ob sogenannte Fat-Tails, also relativ wahrscheinliche, extreme Ereignisse existieren.

Abbildung 219: Beispielhaftes Histogramm mit Extremwerten
• Verteilung
Insgesamt gibt die Form der Verteilung sehr viel „Gefühl“ dafür, wie die Wahrscheinlichkeiten verteilt sind. Welche Bereiche sind wahrscheinlich („hohe Balken“) und welche nicht.
• „Mehrgipfligkeit“
Unter Umständen können auch mehrgipflige Dichtefunktionen entstehen. Dies kommt zustande, wenn einzelne Ereignisse mit relativ hoher Eintrittswahrscheinlichkeit und gleichzeitig hoher Schadenswirkung existieren. Dadurch wird die Menge der Realisationen in zwei Gruppen „eingeteilt“, die Realisationen bei denen der Schaden gewirkt, und die Gruppe, bei denen er nicht gewirkt hat. Wie diese Gruppen zueinander sind, ist aus einem Histogramm auch auf dem ersten Blick zu sehen.
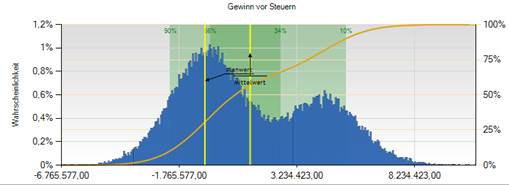
Abbildung 220: Beispiel eines mehrgipfligen Histogramms