Die Normalverteilung ist eine symmetrische, stetige Wahrscheinlichkeitsverteilung, die mit den beiden Parametern Erwartungswert (siehe 19.7) und Standardabweichung (siehe 19.9) definiert wird.
Auszug aus Wikipedia (https://de.wikipedia.org/wiki/Normalverteilung):
Die Normal- oder Gauß-Verteilung (nach Carl Friedrich Gauß) ist ein wichtiger Typ stetiger Wahrscheinlichkeitsverteilungen. Ihre Wahrscheinlichkeitsdichte wird auch Gauß-Funktion, Gaußsche Normalverteilung, Gaußsche Verteilungskurve, Gauß-Kurve, Gaußsche Glockenkurve, Gaußsche Glockenfunktion, Gauß-Glocke oder schlicht Glockenkurve genannt.
Die besondere Bedeutung der Normalverteilung beruht unter anderem auf dem zentralen Grenzwertsatz, dem zufolge Verteilungen, die durch Überlagerung einer großen Zahl von unabhängigen Einflüssen entstehen, unter schwachen Voraussetzungen annähernd normalverteilt sind.
Die Abweichungen der (Mess-)Werte vieler natur-, wirtschafts- und ingenieurswissenschaftlicher Vorgänge vom Mittelwert lassen sich durch die Normalverteilung (bei biologischen Prozessen oft logarithmische Normalverteilung) entweder exakt oder wenigstens in sehr guter Näherung beschreiben (vor allem Prozesse, die in mehreren Faktoren unabhängig voneinander in verschiedene Richtungen wirken).
Zufallsgrößen mit Normalverteilung benutzt man zur Beschreibung zufälliger Vorgänge wie:
• zufällige Messfehler,
• zufällige Abweichungen vom Nennmaß bei der Fertigung von Werkstücken,
• Beschreibung der brownschen Molekularbewegung.
In der Versicherungsmathematik ist die Normalverteilung geeignet zur Modellierung von Schadensdaten im Bereich mittlerer Schadenshöhen.
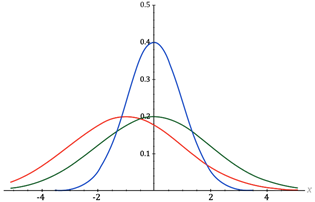
Abbildung 249: Dichtefunktionen der Normalverteilung ![]() :
:
![]() (blau),
(blau), ![]() (grün)
und
(grün)
und ![]() (rot)
(rot)